السلام عليكم و رحمة الله و بركاته
الحمد لله على توفيقه على إعداد هذا البرنامج المتعلق بجدول كارنوف Karnaugh Map
موريس كارنوف Maurice Karnaugh عالم رياضيات أمريكي استعمل طريقة تبسيط المعادلات المنطقية المستعملة في مجال الرياضيات الثنائية أو ما يعرف بالجبر المنطقي أو جبر بول Boolean Algebra
يرتكز جبر بول على اختزال المعادلات المنطقية باستعمال البوابات المنطقية logic gates ،يتم استعمال جدول الحقيقة لمعرفة حالة الخرج الكهربائي للمتغيرات الكهربائية
نحصل إذن من خلال جدول الحقيقة على المعادلة الكهربائية لدائرة كهربائية معينة قد تحتوي على متغيرة أو مجموعة من المتغيرات الكهربائية
يصعب استعمال المعادلة الكهربائية المستنبطة من جدول الحقيقة في حالة وجود العديد من المتغيرات و لذلك يتم اختزال المعادلة المنطقية باستعمال خريطة كارنوف Karnaugh Map
يتم تركيب حالة المتغيرات الكهربائية في جدول كارنوف باستعمال الأرقام الثنائية : 0 و 1
لحساب عدد خانات الجدول نستعمل المعادلة الرياضية التالية :
N=2n
N= مجموع عدد خانات الجدول
n= عدد المتغيرات بحيث a تعتبر متغيرة واحدة تقبل الحالة المنطقية 0 أو 1 فقط
يختلف وضع المتغيرات حسب عدد خانات الجدول كما يمكن تعريف المتغيرات بمسميات مختلفة ، فتستطيع أن تعطي للمتغيرة اسم حرف ك أ ، ب ، ت ، .... أو a,b, c , t ,f v ...أو تعطيها اسم كمفتاح الغرفة ، زر الإنارة لكن استعمال الحروف بدل الكلمات أفضل
استعمال طريقة كارنوف لإختزال المعادلة الرياضية:
تهدف طريقة كارنوف في استعمال جدول يحتوي على حالة مجموعة من المتغيرات الكهربائية و يعتمد على طريقة الطي النظري لتكوين المجموعات القابلة للتبسيط
تعتمد طريقة الطي النظري على طي جدول مخطط كارنوف أفقيا و عموديا لإستخلاص جميع الخانات التي تقبل التطابق
عند عملية الطي النظري نجد لكل خانة من خانات جدول كارنوف Karnaugh Map خانة أخرى تماثلها
لنعتمد الجدول التالي :
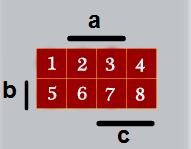
الجدول يتكون من أربع خانات في كل سطر
لو قمنا بطي الجدول أفقيا لوجدنا تماثل بين الخانة 1 مع الخانة 4 ، و تماثل بين الخانة 2 مع الخانة 3
لو قمنا بطي الجدول عموديا لوجدنا تماثل بين الخانة 1 مع الخانة 5 ، و تماثل بين الخانة 2 مع الخانة 6، و تماثل بين الخانة 3 مع الخانة 7، و تماثل بين الخانة 4 مع الخانة 8
لنفترض حالة المتغيرات في الجدول التالي :
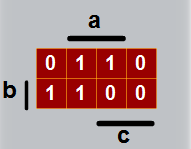
نجد التماثل بين الخانة 2 مع الخانة 3 في الطي الأفقي
و نجد التماثل بين الخانة 2 مع الخانة 6 في الطي العمودي
نعتبر التطابق بين الخانات إذا كانت حالة الخانات المتماثلة تساوي 1
لا تطابق بين الخانة رقم 5 و الخانة 8 في الطي الأفقي لأن حالة إحداهما تساوي 1 و حالة الأخرى تساوي 0
لا تطابق بين الخانة رقم 5 و الخانة 1 في الطي العمودي لأن حالة إحداهما تساوي 1 و حالة الأخرى تساوي 0
و هذا يؤكد ضرورة وجود الرقم 1 في الخانات المتماثلة لإعتبار التطابق
إذا توفر التطابق بين الخانات المتماثلة في الجدول يمكن تكوين المجموعات المتماثلة
يتم الجمع بين خانتين متطابقتين في الجدول كما يمكن الجمع بين أربع خانات متطابقة
في حالة الجمع بين أربع خانات متطابقة يفترض أن تكون هذه المجموعة أربع خانات متلاصفة على شكل سطر أو مربع
يمكن تكوين مجموعة في التطابق العمودي لكل خانة سبق استعمالها في التطابق الأفقي كما في مثالنا فقد استعملت الخانة رقم 2 في التطابق الأفقي و العمودي
يتم اختزال المتغيرات في حالة التطابق فتبقى المتغيرات التي لم يتغير وضعها و تزول المتغيرات التي تغير وضعها المنطقي
اعتبرت في البرنامج ما يلي :
a = b = c = d = 1
A = B = C = D = 0
و هذا الإعتبار لتسهيل عملية الكتابة لعدم توفر خاصية كتابة ــــ فوق كل متغيرة تساوي 0 في الحواسيب المعتمدة حاليا
أتمنى أنكم استوعبتم اختصارات جبر بول في اختزال المعادلات المنطقية
إذا عدنا الى عملية التطابق الأفقي لحصلنا على ما يلي :
Q = a.B.C + a.B.c
ما يمكن كتابته على النحو التالي :
Q = aBC + aBc
عملية الإختزال حسب جبر بول تعطينا ما يلي :
Q = aB . ( C + c )
و نعلم أن :
1 = ( C + c )
و يمكن اختزاله إذن لنحصل على :
Q = aB
هذا بطبيعة الحال ما حصلنا عليه في التطابق الأفقي للجدول بالنسبة للخانة 2 و 3
و ينبغي تطبيق قواعد جبر بول في اختزالات التطابقات التي نحصل عليها في الجدول
يتم كتابة جميع الإختزالات الممكنة من خلال مخطط كارنوف كما يتم كتابة المتغيرات التي لم يتم اختزالها
يشترط لكل خانة لم يتوفر تطابقها الأفقي أن لا تحسب في المعادلة إلا مرة واحدة سواء وجد تطابقها العمودي أم لم يوجد
البرنامج يقوم باختزال تطابق خانتين فقط و قد تجد فيه معادلات تحتاج للإختزال لأن البرنامج لا يقوم باختزال أربع خانات متلاصقة
يمكن التعليق على البرنامج في المنتدى
برنامج تدريبات على جدول كارنوف
لتحميل البرنامج على الرابط التالي :



